Stichprobenrechner
Erleichtern Sie sich die Arbeit mit unserem Stichprobenrechner und lesen Sie viel Wissenswertes zur Berechnung der Stichprobengröße. Sie möchten gerne noch mehr erfahren? Dann entdecken Sie unsere Features und Umfragevorlagen, die belastbare Ergebnisse bringen.

Wie viele Teilnehmende benötigen Sie für Ihre Umfrage? Die Ermittlung der Stichprobengröße kann selbst für Statistiker:innen eine Herausforderung darstellen. Mit unserem Stichprobenrechner können Sie ganz leicht ermitteln, wie viele Beantwortungen für Ihre Umfrage nötig sind.
Stichprobengröße berechnen
Populationsgröße
Konfidenzniveau (%)
Fehlerspanne (%)
Stichprobengröße
0
Erhalten Sie fundiertere Antworten
SurveyMonkey-Genie prüft und bewertet den Entwurf Ihrer Befragung und erkennt mögliche Probleme und Stolpersteine im Umfrageaufbau oder Frageformat. Ihnen werden dann Optimierungen vorgeschlagen, um eine höhere Abschlussquote zu erzielen.
Was bedeutet Stichprobengröße bzw. Stichprobenumfang?
Die Anzahl der abgeschlossenen Beantwortungen für Ihre Erhebung ist die Stichprobengröße, auch Stichprobenumfang genannt. Stichprobe deshalb, weil sie nur einen Teil der Personen (oder Zielpopulation) repräsentiert, deren Meinungen oder Verhalten Sie erfragen möchten. Eine Möglichkeit der Probennahme ist die Verwendung einer sogenannten Zufallsstichprobe. Hierbei werden die Befragten vollkommen zufällig aus der Gesamtpopulation ausgewählt.
Mit dieser Definition tauchen wir nun tiefer in die folgenden Themen ein:
- die verschiedenen Möglichkeiten, die Ergebnisse für Ihre Stichprobe zu interpretieren
- die Formel zur Berechnung der Stichprobengröße
- weshalb eine angemessene Stichprobengröße für eine Umfrage wichtig ist
- wie sich die Bedeutung der Stichprobengröße je nach Umfragetyp unterscheidet
Welche Daten benötigen Sie für die Berechnung der Stichprobengröße?
Im Folgenden erklären wir drei Hauptbegriffe, die Sie kennen sollten, um die Stichprobengröße zu berechnen und sie in den richtigen Zusammenhang zu setzen:
Populationsgröße: Die Gesamtanzahl der Personen der Gruppe, die Sie untersuchen möchten. Wenn wir eine zufällig ausgewählte Stichprobe der in Deutschland wohnhaften Menschen nehmen würden, läge die Populationsgröße bei etwa 84 Millionen. Analog dazu ist die Populationsgröße bei einer Umfrage in Ihrem Unternehmen die Gesamtanzahl Ihrer Mitarbeitenden.
Sie haben die Wahl: Senden Sie Ihre Befragung an eine kleine oder große Gruppe – mit unserem Online-Audience-Panel.
Die Fehlerspanne: Ein Prozentwert, der besagt, in welchem Maße Sie erwarten können, dass Ihre Umfrageergebnisse für die Ansichten der betrachteten Gesamtpopulation repräsentativ sind. Je kleiner die Fehlerspanne, desto näher liegen Sie bei einem bestimmten Konfidenzniveau an der genauen Antwort.
Konfidenzniveau der Stichprobe: Ein Prozentsatz, der angibt, wie sicher Sie sich sein können, dass die Population eine Antwort in einem bestimmten Bereich auswählen würde. Beispielsweise bedeutet ein Konfidenzniveau von 95 % für Sie eine Sicherheit von 95 %, dass die Ergebnisse zwischen den Zahlen X und Y liegen.
Wenn Sie die für Sie geltende Fehlerspanne berechnen möchten, testen Sie unseren Fehlermargenrechner.
Wie berechnen Sie die Stichprobengröße?
Fragen Sie sich, wie das geht: die Stichprobengröße berechnen? Wenn Sie diesen Wert selbst berechnen möchten, verwenden Sie folgende Formel:
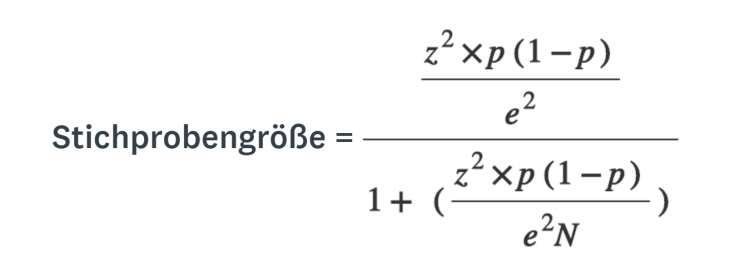
N = Populationsgröße • e = Fehlerspanne (Prozentsatz im Dezimalformat) • z = Z-Wert
Der Z-Wert entspricht der Standardabweichung, die ein bestimmter Anteil vom Mittelwert entfernt ist. Den jeweils richtigen Z-Wert können Sie der nachstehenden Tabelle entnehmen:
| Gewünschtes Konfidenzniveau | Z-Wert |
| 80 % | 1,28 |
| 85 % | 1,44 |
| 90 % | 1,65 |
| 95 % | 1,96 |
| 99 % | 2,58 |
Hierauf müssen Sie beim Berechnen des Stichprobenumfangs achten:
- Wenn Sie eine kleinere Fehlerspanne möchten, bedeutet dies, dass Sie bei gleicher Population eine größere Stichprobengröße benötigen.
- Je höher das gewünschte Konfidenzniveau der Stichprobe, desto größer muss die Stichprobengröße sein.
Wie sich die Ermittlung der Stichprobengröße je nach Umfragetyp ändert
Hat die statistische Signifikanz der Stichprobengröße eine Bedeutung? Hier gibt es eine einfache Regel: Je größer die Stichprobengröße, desto höher ihre statistische Signifikanz. Heißt, das Risiko, dass Ihre Ergebnisse einfach nur durch Zufall entstanden sind, ist geringer.
Müssen Sie die statistische Signifikanz berechnen? Dann nutzen Sie doch einfach unseren A/B-Test-Rechner.
Vielleicht fragen Sie sich, ob die statistische Signifikanz einer Stichprobengröße denn von Bedeutung ist. Und die Antwort ist: Das hängt vom Einzelfall ab. Auch mit Stichprobengrößen, die nicht die allgemeine Population repräsentieren, können Sie wertvolle Antworten gewinnen. Dies gilt beispielsweise für Kundenfeedback, das über Befragungen erfasst wird. Die statistische Signifikanz der Stichprobengröße spielt hier keine Rolle. Allein, dass Sie Ihren Kunden zuhören, eröffnet Ihnen wertvolle Perspektiven zur Verbesserung Ihrer Geschäftszahlen.
Ein Gegenbeispiel sind politische Meinungsumfragen. Hier müssen Sie mit großer Sorgfalt sicherstellen, dass die richtige Stichprobengröße befragt wird: Sie muss ausgeglichen sein, damit sie die Gesamtpopulation widerspiegelt. Im Folgenden haben wir für Sie einige Anwendungsbeispiele zusammengestellt, aus denen Sie erkennen können, ob die statistische Signifikanz der Stichprobengröße einen Unterschied macht oder nicht.
Wirkung der Umfragewerte auf die Genauigkeit der Ergebnisse
| Höherer Wert | Niedrigerer Wert | |
| Populationsgröße | Genauigkeit nimmt ab | Genauigkeit nimmt zu |
| Stichprobengröße | Genauigkeit nimmt zu | Genauigkeit nimmt ab |
| Konfidenzniveau | Genauigkeit nimmt zu | Genauigkeit nimmt ab |
| Fehlerspanne | Genauigkeit nimmt ab | Genauigkeit nimmt zu |
Mitarbeiter- und Personalbefragungen
Arbeiten Sie an einer Umfrage zur Mitarbeiterzufriedenheit? Alle Personalbefragungen liefern wertvolles Feedback dazu, wie die Mitarbeitenden die Arbeitsumgebung in Ihrem Unternehmen empfinden. Mit einer Stichprobengröße, die statistisch signifikant ist, erhalten Sie eine ganzheitlichere Sicht auf die Beschäftigten im Allgemeinen. Aber auch wenn die Stichprobengröße keine statistische Signifikanz hat, ist es wichtig, die Umfrage zu senden. Denn Personalbefragungen können Ihnen wertvolles Feedback dazu liefern, wie Sie den Arbeitsplatz für Ihre Mitarbeitenden noch besser gestalten können.
Umfragen zur Kundenzufriedenheit
Wie schon bereits erwähnt, müssen Umfragen zur Kundenzufriedenheit nicht unbedingt eine statistisch signifikante Stichprobengröße haben. Zwar ist es von Bedeutung, dass die Beantwortungen genau sind und die Meinung Ihrer Kunden widerspiegeln, aber wirklich wichtig ist, sich jede Antwort einer Umfrage zur Kundenzufriedenheit genau anzusehen. Denn jedes Feedback, positives wie negatives, ist relevant.
Marktforschung
Wenn Sie eine Marktforschungsumfrage durchführen, kann es einen großen Unterschied machen, ob die Stichprobengröße statistisch signifikant ist oder nicht. Über Marktforschungsumfragen können Sie mehr über Ihre Kunden und Ihren Zielmarkt erfahren. Das heißt, dass Sie mithilfe von Stichprobengrößen mit statistischer Signifikanz Erkenntnisse über Ihren Zielmarkt insgesamt gewinnen können. Außerdem erreichen Sie so bei den erhaltenen Informationen die höchste Genauigkeit.
Bildungsumfragen
Für Umfragen im Bildungsbereich empfehlen wir, statistisch signifikante Stichprobengrößen zu verwenden, die die Population widerspiegeln. Angenommen, Sie planen für Ihre Schule Änderungen anhand von Schülerfeedback zu Schule, Lehrkräften und anderen Beschäftigten. Dann bietet eine Stichprobengröße mit statistischer Signifikanz die Möglichkeit, genau die Ergebnisse zu erhalten, mit denen Sie die Schule zum Erfolg führen können. Wenn Sie aber einfach nur Feedback von den Schüler:innen haben möchten, um zu wissen, was diese so denken, und nicht unbedingt Änderungen vornehmen möchten, dann ist die statistische Signifikanz der Stichprobengröße unter Umständen nicht so wichtig.
Gesundheit Umfragen
Bei Erhebungen im Gesundheitswesen kann eine statistisch signifikante Stichprobengröße Sie dabei unterstützen, die Gesundheitsthemen zu erkennen, die für Ihre Patienten von größerer Bedeutung sind als andere. Möglicherweise können Sie so auch zu Insights im Bereich der Medizinforschung kommen. Wenn Sie die Befragungen im Gesundheitswesen einsetzen, um Gründe für Patientenzufriedenheit zu erfahren oder um die Patienten zu ihrer regelmäßigen Versorgung zu befragen, ist die statistische Signifikanz der Stichprobengröße unter Umständen von geringerer Bedeutung. Denn Sie erhalten über die Umfrage trotzdem wertvolle Informationen von Ihren einzelnen Patientinnen und Patienten zu deren Bedürfnissen und Erfahrungen.
Freizeitumfragen
Vielleicht möchten Sie allgemein immer mal wieder Befragungen an Ihre Freunde, Kollegen oder Familie senden. In diesem Fall müssen wir uns anschauen, was Sie damit erreichen wollen: Wenn Sie die Ergebnisse als Beleg nutzen möchten, ist es wichtig, dass die Stichprobengröße statistisch signifikant ist. Wenn Sie die Umfrage aber eigentlich nur zum Spaß versenden, schadet es niemandem, wenn sie nur an wenige Leute geht.
Benötigen Sie weitere Beantwortungen?
Schätzen Sie nicht einfach nur, wie viele Personen an Ihrer Befragung teilnehmen sollten und verzetteln Sie sich nicht in Wahrscheinlichkeitsstichproben oder Modellen zur Wahrscheinlichkeitsverteilung. Nutzen Sie stattdessen unseren Stichprobenrechner. Machen Sie sich mit Stichprobenverzerrung, Stichprobengröße und statistischer Signifikanz der Stichprobengröße vertraut und damit, wie Sie mehr Beantwortungen erzielen können. Dann bekommen Sie sehr schnell das notwendige Wissen, um für Ihre Erhebung eine höhere Datenqualität zu erreichen.
Wenn der Stichprobenumfangs-Rechner angibt, dass Sie mehr Befragte benötigen, können wir helfen. Teilen Sie uns mit, welche Population Sie anvisieren, und wir finden für Sie die richtigen Menschen, die Ihre Umfragen beantworten. Da in SurveyMonkey Audience Millionen qualifizierte Umfrageteilnehmende bereitstehen, ist es für Sie leicht, sofort Antworten von Menschen auf der ganzen Welt, von nahezu jedem, zu erhalten.
Weitere Ressourcen entdecken

Umfragevorlagen zur Kundenzufriedenheit
Mit unseren kostenlosen Vorlagen für Umfragen zur Kundenzufriedenheit sparen Sie Zeit und werden gleichzeitig mit neuen Ideen versorgt. Beschaffen Sie sich noch heute das Feedback, das Sie benötigen.

Erhalten Sie umsetzbares Feedback mit Online-Bewertungsformularen
Nutzen Sie die Chancen von Feedback mit Hilfe der Online-Bewertungsformulare von SurveyMonkey. Starten Sie noch heute mit unserer Formularerstellung!

Über den Net Promoter Score hinaus: Warum Kontext so entscheidend ist
Zeigt die Auswirkungen kultureller Unterschiede auf den globalen Net Promoter® Score und beinhaltet eine kontextbezogene Analyse der generellen NPS-Daten.

Erfahren Sie, wie Box sein Team durch Kundendaten stärkt
Überzeugen Sie sich davon, wie Box SurveyMonkey nutzt, um eine 360-Grad-Sicht der Customer Journey zu erhalten und Feedback zentral zu erfassen.
Benötigen Sie mehr Beantwortungen für Ihre Umfrage?
Nutzen Sie SurveyMonkey Audience, unser globales Umfragepanel aus Millionen Menschen, die Ihnen gerne ihre Meinung mitteilen.
